Brennstoffzellen

Brennstoffzellengrundprinzip

Die Brennstoffzelle ist ein idealer, chemischer Reaktor, in dem die chemische Energie von Wasserstoff und Sauerstoff  ohne Verbrennung in elektrische Energie und Wärme umgewandelt wird. Deshalb spricht man von „kalter Verbrennung“. Die Brennstoffzelle ist ein Energiewandler.

 

Thermodynamische Grundlagen der Brennstoffzelle

Die „Enthalpie“ ist die innere Energie der Stoffe und wird mit H widergegeben.
Die Enthalpieänderung ∆H ist die „Quelle“, aus der in einer Brennstoffzelle elektrische Energie und Wärmeenergie entnommen werden. Je größer der ∆H-Wert ist, desto größer auch die freigesetzte Energie. Der ∆H-Wert hat ein negatives Vorzeichen, sobald Energie freigesetzt wird. In einem solchen Fall handelt es sich um eine exotherme chemische Reaktion. Positive ∆H-Werte bedeuten dagegen, dass Energie hinzugefügt wird. In diesem Fall handelt es sich um eine endotherme chemische Reaktion.
Bei Brennstoffzellen sind die ∆H-Werte stets negative. Dort wird also immer Energie freigesetzt, die aus der chemisch gespeicherten Energie in den Reaktanten Wasserstoff und Sauerstoff stammt.
Je größer der ∆H-Wert ist, desto größer auch die freigesetzte Energie.
Als Entropie S wird die Unordnung eines Systems bezeichnet. Bei festen Stoffen ist sie (bei konstanter Temperatur) kleiner als bei flüssigen und viel kleiner als bei gasförmigen Stoffen. In einer Brennstoffzelle entsteht aus zwei gasförmigen Stoffen, d.h. aus Wasserstoff und Sauerstoff, ein flüssiger Stoff, nämlich Wasser.

	H2	0.5 O2	H2O	Änderung
Enthalpie	0	0	-285.83 kJ	ΔH = -285.83 kJ
Entropie	130.68 J/K	0.5 x 205.14 J/K	69.91 J/K	TΔS = -48.7 kJ

Den Zusammenhang zwischen Entropie S und Enthalpie H beschreibt die sog. Gibbs-Helmholz-Gleichung ∆G = ∆H – T ∆ S. Findet keine Entropieänderung statt, dann ist ∆G = ∆H. Dies bedeutet, dass die ganze Enthalpie des Systems in Energie umgewandelt wird [1].
Der theoretische Wirkungsgrad kann dabei aus der Gibbs-Helmholz-Gleichung errechnet werden. In der folgenden Tabelle 1 wird dieser Wirkungsgrad für verschiedene Brennstoffe berechnet.

H2:  ∆G = 237,5 KJ/mol ∆H=286,0 kJ/mol ηel=∆G/∆H = 237,5 kJ/286,0 kJ=0,83 (83%)	CO:     ∆G = 257,8 KJ/mol        ∆H = 283,1 kJ/mol ηel = ∆G/∆H = 0,909 (90,9%)
CH4:  ∆G = 818 KJ/mol ∆H = 890,8 kJ/mol ηel = ∆G/∆H = 818,4 kJ/890,8 kJ=0,919 (91,9%)	CH3OH:     ∆G = 702,5 KJ/mol   ∆H = 726,6 kJ/mol ηel = ∆G/∆H = 0,967 (96,7%)

Tabelle 1: Durchschnittswerte von ∆G und ∆H für verschiedene Brennstoffe (bei Normalbedingungen)
Unter Normalbedingungen weisen die chemischen Elemente in Bezug auf Enthropie, Enthalpie und freigesetzte Energie, die im Folgenden in Tabelle 2 angegebenen Werte auf. Diese Elemente können als Brennstoffe einer SOFC-Brennstoffzelle eingesetzt werden.

Chemische Elemente	Aggregatszustand	H0 [kJ/mol]	S0  [kJ/molK]	G0 [kJ/mol]
H	Gas	217,9	0,114	203,3
H2	Gas	0	0,130	0
O	Gas	247,5	0,161	231,8
O2	Gas	0	0,205	0
H2O	Flüssig	-285,8	0,0699	-237,2
H2O	Gas	-241,8	0,1888	-228,6
C	Fest	0	0,006	0
CH4	Gas	-74,9	0,186	-50,8
CO	Gas	-110,5	0,197	-137,2
CO2	Gas	-393,5	0,213	-394,4
CH3OH	Flüssig	-238,7	0,1268	-166,4

Tabelle 2: Enthalpie H₀, absolute Entropie S₀ und Gibbs’sche  freie Energie G0 (bei 25 ˚C und 1 atm)
Die elektrischen Parameter von Brennstoffzellen
In einer SOFC-Brennstoffzelle treten verschiedene Spannungsverluste auf, die sich wie folgt berechnen lassen
∆U = ∆U_rev + ∆D_U + ∆U_R + ∆U_Diff
∆ U_rev  – reversible Spannungsdifferenz
∆ U_D  –  Durchtrittsspannung (aufgrund des Durchtritts der Elektronen durch die Phasengrenzfläche zwischen Elektrolyt und Elektrode verursacht)
∆U_R  –  Widerstandsspannung („Ohmsche Verluste“ – durch Stromstärkeerhöhung)
∆U_Diff  – Konzentrationsspannung (die Nachführung der Geschwindigkeit der Endukte ist kleiner als die der elektrochemischen Reaktion)  [2].

Abb. 1: Spannungsverluste in der SOFC-Brennstoffzelle
Die theoretische Maximalspannung (thermoneutrale Spannung) wird in der Realität durch die auftretenden Verluste auf die Zellspannung abgesenkt, wie in Abb. 2 dargestellt.

Abb. 2: Schematische Darstellung einer Strom/Spannungskennlinie
Im Weiteren werden die verschiedenen, in Abb. 2 dargestellten Spannungszustände berechnet.
Die thermoneutrale oder enthalpische Spannung kann unter Normalbedingungen (T₀=298,15K und P₀=1,013 bar) wie folgt berechnet werden:

n  – Elektronenanzahl
F – Faraday-Konstante       F = e∙Na = 1,6022∙10-¹⁹C x 6,022∙10²³ 1/mol = 96487 C/mol
Na – Avogadro-Konstant
Werte der Enthalpieänderung ∆H:

∆H₀ = -241,8 kJ/mol  (H₂O gasförmig)

∆H₀ = -285,6 kJ/mol  (H₂O flüssig)

Die freie Reaktionsenthalpie ∆G₀ der Gesamtreaktion (max. gewinnbare Arbeit)

∆G₀ = -228,6 kJ/mol  (H₂O gasförmig)

∆G₀ = -237,3 kJ/mol  (H₂O flüssig)

Mit Hilfe der maximalen, elektrischen Arbeit (Gibbs’sche Enthalpie) kann das Standardpotenzial berechnet werden:

Die Nernstspannung reduziert das Standardpotenzial durch die Änderung von Normalbedingungen (Druck und Temperatur ändern).
Die Nernstspannung:     Die Spannung als Stromfunktion
Die Stromdichte hängt hauptsächlich von der effektiven Zellfläche ab. Dies wird durch die poröse Gestaltung der Oberfläche der Elektroden erreicht:

U(i) = U-R∙i

i  – Stromdichte [mA/cm²]
R  – flächenspezifischer Widerstand (Ohmsche + Polarisationsverluste) [mΩ]
U – Nernst-Potential [mV]

Abb. 3: Das Arbeitsprinzip einer Brennstoffzelle und das Äquivalent eines Stromkreises [3]
Durch die verschiedenen Leitwerte für Elektrolyte (Elektronik und Ionik) gibt es zwei Widerstandsarten in der Brennstoffzelle (siehe auch Abb. 3):
R₁  –  ionischer Widerstand
R₂   – elektrischer Widerstand
R₃  – externe Last
Mit Hilfe des Ohm- und Kirchhoff’schen Gesetzes kann man den Stromverlauf in der BZ ermitteln :

η_f  – Brennstoffnutzungsfaktor (dieser Parameter definiert das Brennstoffverhältnis, welches für die Herstellung von elektrischem Strom genutzt wird).

Die Brennstoffzellenspannung ist hauptsächlich abhängig vom Brennstoffnutzungsfaktor (der in der BZ-Anlage mit η_f =0,8 angesetzt wird) und vom maximalen Strom:

Brennstoffzellenspannung

Der maximale Strom ist abhängig von der Strömung der Brennstoffe:

Die Brennstoffzelle hat verschiedene Flächenausdehnungen (100-900)cm². Strom und Widerstand sind abhängig von der aktiven Zellfläche.
U_max  –  maximale Spannung
i_max  – Stromdichte
η_f  – Brennstoff-Nutzungs-Faktor
r₁  – spezifischer, interner ionischer Widerstand
r₂   – spezifischer, interner elektrischer Widerstand
Wirkungsgrad
Der Wirkungsgrad einer Brennstoffzelle hängt von chemischen, thermischen und elektrischen Parametern ab und lässt sich wie folgt berechnen:
Wirkungsgrad
η= W_el + W_th / W_ch
Thermodynamische Daten für die Brennstoffzelle (unter Normalbedingungen) sind in Tabelle 3 angegeben. Mit folgender Formel lässt sich der ideale  Wirkungsgrad einer SOFC-Brennstoffzelle berechnen :

(das Produktwasser liegt gasförmig vor)

Brennstoff	Reaktion	n	∆H  [kJ/mol]	∆G  [kJ/mol]	E [V]	hth [%]
Wasserstoff	H2+1/2O2→H2O	2	-286,0	-237,3	1,229	83,0
Kohlenmonoxid	CO+1/2O2→CO2	2	-283,1	-257,2	1,066	90,9
Ameisensäure	HCOOH+1/2O2→CO2+H2O	2	-270,3	-285,5	1,480	105,6
Methanol	CH3OH+3/2O2→CO2+2H2O	6	-726,6	-702,5	1,214	96,7
Methan	CH4+2O2→CO2+2H2O	8	-890,8	-818,4	1,060	91,9

h_th – idealer Wirkungsgrad
Tabelle 3: Thermodynamische Daten für die Brennstoffzelle (unter normalen Bedingungen)
Der Heizwert H_w des Wasserstoffs beträgt 39,4k Wh/kg (oberster Heizwert) bzw. 32 kWh/kg (unterster Heizwert). Weil aber 1k Wh = 3,6 MJ entspricht, erhalten wir die folgenden MJ-Werte:
39,4 kWh/kg∙3,6 MJ/kWh = 141,8 MJ/kg  bzw.
32 kWh/kg ∙3,6 MJ/kWh = 118,8 MJ/kg
Das molare Gewicht von Wasserstoff beträgt 2 g. Durch die Verbrennung von einem Mol Wasserstoff entsteht also eine Energiemenge von:
141,8∙(2/1000) = 0,2836 MJ = 283,6 kJ  (H₂O – gasförmig)
118,8∙(2/1000) = 0,2376 MJ= 237,6 kJ  (H₂O – flüssig)
Die Abhängigkeit des Wirkungsgrades von der Betriebstemperatur und der Zellspannung wird in Tabelle 4 verdeutlicht

Betriebstemperatur	∆G	hges	Zellspannung
[˚C]	[kJ/mol]	[%]	[V]
100	-225.3	79	1,17
200	-220,4	77	1,14
400	-210,3	74	1,09
600	-199,6	70	1,04
800	-188,6	66	0,98
1000	-177,4	62	0,92

Tabelle 4: Parameter der SOFC-Brennstoffzelle
Je größer die freigesetzte Energie ∆G , desto größer auch der Gesamtwirkungsgrad, wobei ∆G temperatur­abhängig ist.
In der Praxis wird die Zielspannung einer Brennstoffzelle benutzt, um den elektrischen Wirkungsgrad zu ermitteln.

U_rev  – theoretische (ideale) Zellspannung
U_z  – Zielspannung am Betriebspunkt
Der Gesamtwirkungsgrad einer Brennstoffzelle für einen bestimmen Betriebspunkt ist abhängig von einer Temperatur T und einem Druck P:

 

 

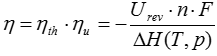
[1] Stratis Karamanolis 2003. Brennstoffzellen – Schlüsselelemente der Wasserstofftechnologie. Vogel Buchverlag,;
[2] Klaus Langeheinecke, Peter Jany, Gerd Thieleke 2008. Thermodynamik für Ingenieure: Ein Lehr- und Arbeitsbuch für das Studium. Vieweg+Teubner Verlag Wiesbaden;
[3] Jroslaw Milewski, Konrad Swirski, Massimo Santarelli, Pierluigi Leone 2011. Advanced Methods of Solid Oxide Fuel Cell Modeling.  Springer